おはようございます!
朝7時からの学習塾
朝塾です。
「円周率が3.05より大きいことを証明せよ」
とても有名な、2003年の東京大学の入試問題です。
時代背景としては、「円周率を3とする」と、小学校の指導要領が話題になっていた頃。そんな諸々のアンチテーゼなんだろうなぁと思っていました。
話を戻します。
この問題、赤本含めた参考書やインターネットなどには、解法がたくさんありますので、高校数学を楽しみたい方はそちらを参考にしてください。
朝塾には、小中学生が多いので、彼らが楽しめるように、
「円周率が3より大きいことを証明せよ」に変えて、考えていきましょう。
最後に、図がありますので、それをみながらの方がわかりやすいと思います。
では、参りましょう!
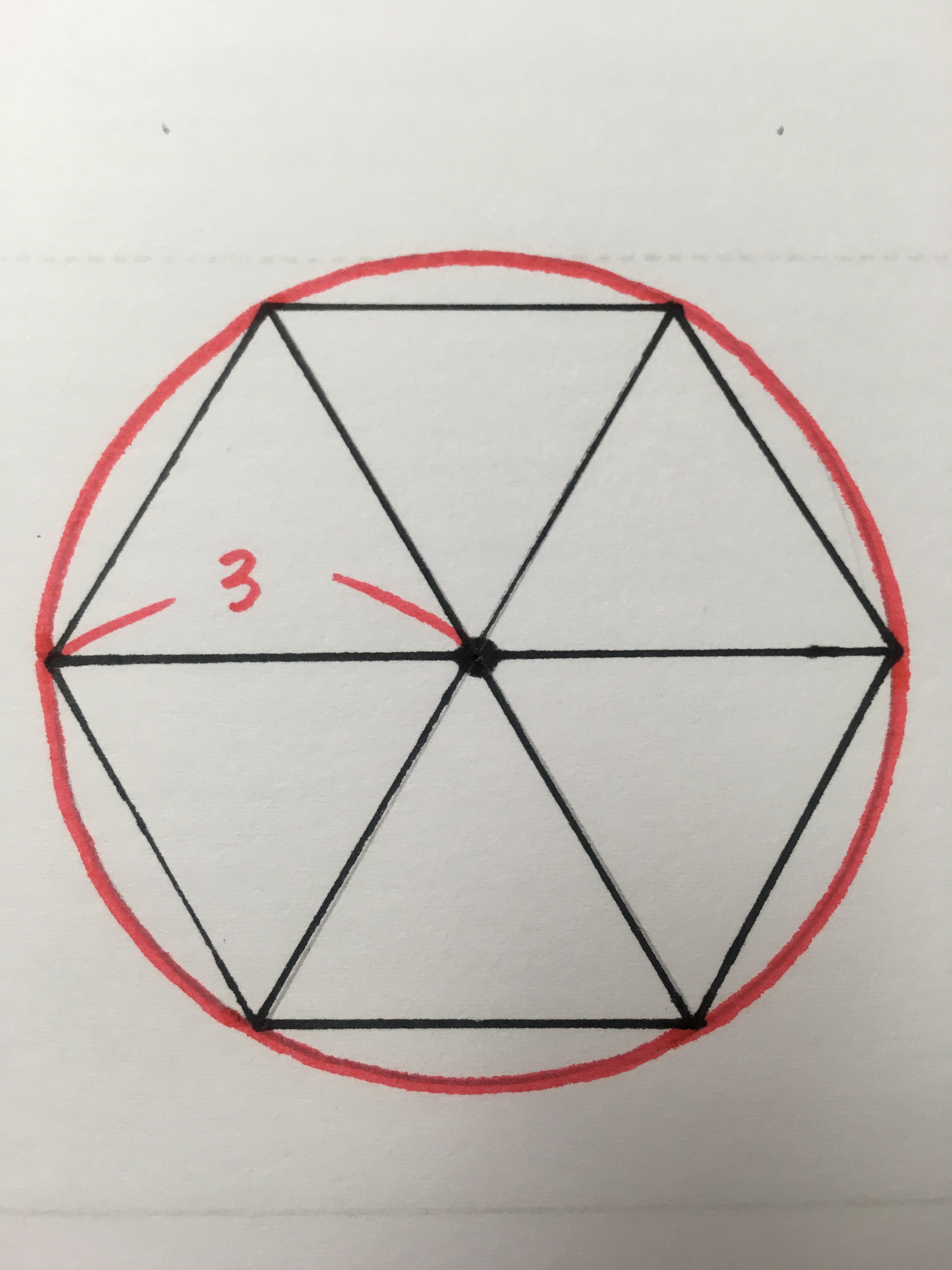
まず、半径が3の円をかきます。
当然、直径は6ですね
その中に、一辺が3の正三角形を6つかきます。
正六角形が出来上がりますね。
正六角形の一番外側の、周りの長さは、3×6=18です。
図にかいた、半径が3の赤い円は、正六角形よりも長さが長いので、円周は、18より大きくなります。
さて。
そもそも、「円周率」とは、何でしょう?
3.14はわかるけれど、円周率って、どういう事?と、改めて聞かれると説明が上手くいかなかったりします。
円周率とは、
「円周の、直径に対する比率」のこと。
3.14…と表されるのは、
例えば、直径が1なら、円周の長さは3.14で、
直径が2なら、6.28で…。ということです。
問題に戻ります。
直径は6でした。
周りの長さは18より長いことがわかりました。
直径を3倍すると18なので、
(6×3=18)
よって、「円周率は、3より大きい」事が、証明できます。
【朝塾では、講師の募集を行っています】
説明会及び講師面接会(要予約)
日時:4月23日9時〜
場所:市川市男女共同参画センター
ご興味のある先生、お電話ください。
ホームページお問合せフォームまたは以下のメールからでも承っております。
一緒に働ける日を楽しみにしております(*^^*)
090 8455 7206
contact@asajuku.jp

